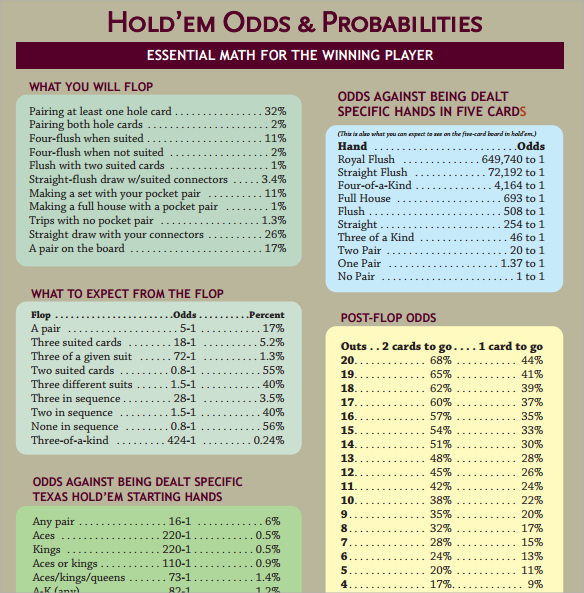
Poker Hand Probabilities
Probabilities in poker Probability means the degree of certainty that a possible event will occur. The classic definition is: 'The probability of an event is the ratio of the number of cases favorable to it, to the number of all cases possible when nothing leads us to expect that any one of these cases should occur more than any other, which. In poker, the probability of each type of 5-card hand can be computed by calculating the proportion of hands of that type among all possible hands. Frequency of 5-card poker hands The following enumerates the (absolute) frequency of each hand, given all combinations of 5 cards randomly drawn from a full deck of 52 without replacement. Pot odds in poker simply means the “price” that it costs you to continue with your hand. For example, if you’re in a hand where the pot is $100 and your opponent bets $50, you’re getting 3 to 1 pot odds to call. The pot is $150 (the $100 that’s already there plus the $50 bet) and it costs $50 to continue. Divide the $150 by $50 to get 3.
POKER PROBABILITIES

- Texas Hold'em Poker
Texas Hold'em Poker probabilities - Omaha Poker
Omaha Poker probabilities - 5 Card Poker
5 Card Poker probabilities
POKER CALCULATOR
- Poker calculator
Poker odds calculator
POKER INFORMATION
- Poker hand rankings
Ranking of poker hands
In poker, the probability of each type of 5-card hand can be computed by calculating the proportion of hands of that type among all possible hands.
Frequency of 5-card poker hands
The following enumerates the (absolute) frequency of each hand, given all combinations of 5 cards randomly drawn from a full deck of 52 without replacement. Wild cards are not considered. The probability of drawing a given hand is calculated by dividing the number of ways of drawing the hand by the total number of 5-card hands (the sample space, five-card hands). The odds are defined as the ratio (1/p) - 1 : 1, where p is the probability. Note that the cumulative column contains the probability of being dealt that hand or any of the hands ranked higher than it. (The frequencies given are exact; the probabilities and odds are approximate.)
The nCr function on most scientific calculators can be used to calculate hand frequencies; entering nCr with 52 and 5, for example, yields as above.
| Hand | Frequency | Approx. Probability | Approx. Cumulative | Approx. Odds | Mathematical expression of absolute frequency |
|---|---|---|---|---|---|
| Royal flush | 4 | 0.000154% | 0.000154% | 649,739 : 1 | |
| Straight flush (excluding royal flush) | 36 | 0.00139% | 0.00154% | 72,192.33 : 1 | |
| Four of a kind | 624 | 0.0240% | 0.0256% | 4,164 : 1 | |
| Full house | 3,744 | 0.144% | 0.170% | 693.2 : 1 | |
| Flush (excluding royal flush and straight flush) | 5,108 | 0.197% | 0.367% | 507.8 : 1 | |
| Straight (excluding royal flush and straight flush) | 10,200 | 0.392% | 0.76% | 253.8 : 1 | |
| Three of a kind | 54,912 | 2.11% | 2.87% | 46.3 : 1 | |
| Two pair | 123,552 | 4.75% | 7.62% | 20.03 : 1 | |
| One pair | 1,098,240 | 42.3% | 49.9% | 1.36 : 1 | |
| No pair / High card | 1,302,540 | 50.1% | 100% | .995 : 1 | |
| Total | 2,598,960 | 100% | 100% | 1 : 1 |
The royal flush is a case of the straight flush. It can be formed 4 ways (one for each suit), giving it a probability of 0.000154% and odds of 649,739 : 1.
When ace-low straights and ace-low straight flushes are not counted, the probabilities of each are reduced: straights and straight flushes each become 9/10 as common as they otherwise would be. The 4 missed straight flushes become flushes and the 1,020 missed straights become no pair.
Note that since suits have no relative value in poker, two hands can be considered identical if one hand can be transformed into the other by swapping suits. For example, the hand 3♣ 7♣ 8♣ Q♠ A♠ is identical to 3♦ 7♦ 8♦ Q♥ A♥ because replacing all of the clubs in the first hand with diamonds and all of the spades with hearts produces the second hand. So eliminating identical hands that ignore relative suit values, there are only 134,459 distinct hands.
The number of distinct poker hands is even smaller. For example, 3♣ 7♣ 8♣ Q♠ A♠ and 3♦ 7♣ 8♦ Q♥ A♥ are not identical hands when just ignoring suit assignments because one hand has three suits, while the other hand has only two—that difference could affect the relative value of each hand when there are more cards to come. However, even though the hands are not identical from that perspective, they still form equivalent poker hands because each hand is an A-Q-8-7-3 high card hand. There are 7,462 distinct poker hands.
Derivation of frequencies of 5-card poker hands
of the binomial coefficients and their interpretation as the number of ways of choosing elements from a given set. See also: sample space and event (probability theory).
- Straight flush — Each straight flush is uniquely determined by its highest ranking card; and these ranks go from 5 (A-2-3-4-5) up to A (10-J-Q-K-A) in each of the 4 suits. Thus, the total number of straight flushes is:
- Royal straight flush — A royal straight flush is a subset of all straight flushes in which the ace is the highest card (ie 10-J-Q-K-A in any of the four suits). Thus, the total number of royal straight flushes is
- or simply . Note: this means that the total number of non-Royal straight flushes is 36.
- Royal straight flush — A royal straight flush is a subset of all straight flushes in which the ace is the highest card (ie 10-J-Q-K-A in any of the four suits). Thus, the total number of royal straight flushes is

- Four of a kind — Any one of the thirteen ranks can form the four of a kind by selecting all four of the suits in that rank. The final card can have any one of the twelve remaining ranks, and any suit. Thus, the total number of four-of-a-kinds is:
- Full house — The full house comprises a triple (three of a kind) and a pair. The triple can be any one of the thirteen ranks, and consists of three of the four suits. The pair can be any one of the remaining twelve ranks, and consists of two of the four suits. Thus, the total number of full houses is:
- Flush — The flush contains any five of the thirteen ranks, all of which belong to one of the four suits, minus the 40 straight flushes. Thus, the total number of flushes is:
- Straight — The straight consists of any one of the ten possible sequences of five consecutive cards, from 5-4-3-2-A to A-K-Q-J-10. Each of these five cards can have any one of the four suits. Finally, as with the flush, the 40 straight flushes must be excluded, giving:
- Three of a kind — Any of the thirteen ranks can form the three of a kind, which can contain any three of the four suits. The remaining two cards can have any two of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of three-of-a-kinds is:
Poker Hand Probabilities
- Two pair — The pairs can have any two of the thirteen ranks, and each pair can have two of the four suits. The final card can have any one of the eleven remaining ranks, and any suit. Thus, the total number of two-pairs is:
- Pair — The pair can have any one of the thirteen ranks, and any two of the four suits. The remaining three cards can have any three of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of pair hands is:
- No pair — A no-pair hand contains five of the thirteen ranks, discounting the ten possible straights, and each card can have any of the four suits, discounting the four possible flushes. Alternatively, a no-pair hand is any hand that does not fall into one of the above categories; that is, any way to choose five out of 52 cards, discounting all of the above hands. Thus, the total number of no-pair hands is:
- Any five card poker hand — The total number of five card hands that can be drawn from a deck of cards is found using a combination selecting five cards, in any order where n refers to the number of items that can be selected and r to the sample size; the '!' is the factorial operator:
This guide is licensed under the GNU Free Documentation License. It uses material from the Wikipedia.
Home > 5 Card Poker probabilities
Brian Alspach
17 January 2000
Abstract:
There are a few 6-card poker games so it is worth looking at probabilitiesfor winning with certain kinds of hands. One chooses the highest ranked5-card poker hand among the 6 cards and values the hand based on the5-card hand. The types of 5-card poker hands in decreasing rank are
- straight flush
- 4-of-a-kind
- full house
- flush
- straight
- 3-of-a-kind
- two pairs
- a pair
- high card
The total number of 6-card poker hands is .
A straight flush is completely determined once the smallest card in thestraight flush is known. There are 40 cards eligible to be the smallestcard in a straight flush. If the smallest card in the straight flush isan ace, then the sixth card may be any of 47 cards. If the smallest cardin the straight flush is any of the other 36 eligible beginning cards,then the sixth card may be any of 46 cards because we cannot use the nextsmallest card in the same suit as the straight flush. Hence, there are6-card hands containing straight flushes.
In forming a 4-of-a-kind hand, there are 13 choices for the rank ofthe quads, 1 choice for the 4 cards of the given rank, and choices for the remaining 2 cards. This implies there are 4-of-a-kind hands.
There are 2 ways to get a full house and we count them separately. Oneway of obtaining a full house is for the 6-card hand to contain 2 setsof triples. There are ways to choose the 2 ranksand 4 ways to choose each of the triples. This gives us full houses of this type. The other way of getting a full houseis for the 6-card hand to contain a triple, a pair and a remaining card ofa third rank. There are 13 choices for the rank of the triple, 12 choicesfor the rank of the pair, and 44 choices for the singleton card. Thereare 4 ways of choosing the triple of a given rank and 6 ways to choose thepair of the other rank. This produces full houses of the latter type. Adding the two numbersyields 165,984 full houses.
To count the number of flushes, we obtain 6-card hands formed from cards in the same suit. Altogether, thereare flushes with 6 cards in the same suit.There are choices for 5 cards in the same suit.There are then 39 choices for a sixth card from a different suit. Thus,there are flushes in 6-card hands, whereprecisely 5 cards are in the same suit. Combining the two gives us207,636 6-card hands containing flushes. Of these, 1,844 are straightflushes whose removal leaves 205,792 flushes.
Let's determine how many sets of 6 distinct ranks correspond to straights.One possible form is ,where x can be any of9 ranks. The other possible form is ,where yis neither x-1 nor x+5. When x is ace or 10, then there are 7choices for y. When x is between 2 and 9, inclusive, there are 6choices for y. This implies there are sets of 6 distinct ranks corresponding to straights. There are then 4choices for each card of the given ranks except we must remove thosechoices producing flushes. There are 4 choices giving all 6 cards inthe same suit. If 5 are in the same suit, there are choices of which 5 ranks will be in the same suit, 4 choicesfor the suit of the 5 cards, and 3 choices for the suit of the remainingcard. So there are choices which give aflush. This means there are 46 - 76 = 4,020 choices not producing aflush. Hence, there are straights of thisform.
We also can have a set of 5 distinct ranks producing a straight whichmeans the corresponding 6-card hand must contain a pair as well. Thereare 10 sets of ranks of the form .There are 5choices of the rank to be paired, 6 choices for the pair, and 4 choicesfor each of the other 4 cards except not all 4 cards can be chosen inthe same suit as either of the cards in the pair. This means there are44 - 2 = 254 choices for the 4 cards. We then have straights of this form. Altogether there are361,620 straights.
In forming a 3-of-a-kind hand, there must be a triple and 3 other cardsall of distinct ranks different from the rank of the triple. There are13 choices for the rank of the triple, and there are choices for the ranks of the other 3 cards. There are 4 choicesfor the triple of the given rank and there are 4 choices for each of thecards of the remaining 3 ranks. Altogether, we have 3-of-a-kind hands.
Next we consider two pairs hands. Such a hand may contain either threepairs, or two pairs plus two remaining cards of distinct ranks. Weevaluate these 2 types of hands separately. If the hand has threepairs, there are ways to choose the ranks ofthe pairs and 6 ways to choose each of the pairs. This produces6-card hands with three pairs.
For the other kind of two pairs hand, there are choices for the two ranks of the pairs and there are ways to choose the ranks of the 2 singletons. There are 6 choicesfor each of the pairs, and there are 4 choices for each of the remaining2 cards. This produces hands of two pairs of the second type. Adding the two gives 2,532,8166-card hands with two pairs.

Now we count the number of hands with a pair. Such a hand must have5 distinct ranks. There are possible setsof 5 ranks. We must remove sets of the form because these correspond to straights. There are 10 such sets leaving1,277 sets of ranks corresponding to a hand with one pair. Given sucha set, there are 5 choices for the rank of the pair, and 6 choices fora pair of the chosen rank. There are 4 choices for each of the remaining4 cards except we cannot choose all 4 to be in the same suit as eitherof the cards forming the pair. Hence, there are 44-2 = 254 choicesfor the remaining 4 cards. This gives us hands with a pair.
We could determine the number of high card hands by removing the handswhich have already been counted in one of the previous categories.Instead, let us count them independently and see if the numbers sumto 20,358,520 which will serve as a check on our arithmetic.
A high card hand has 6 distinct ranks, but does not include straights.So we must eliminate sets of ranks which have 5 consecutive ranks. Indetermining the number of straights above, we derived that there are 71sets of 6 distinct ranks which give straights. There are sets of 6 distinct ranks. Removing the 71 sets correspondingto straights, leaves 1,645 sets of distinct ranks which do not producestraights. There are 4 choices for each of the 6 cards in a given setproducing 46 = 4,096 ways of choosing cards for a given set of ranks.However, some of the choices produce flushes and we must remove them.Clearly there are 4 ways of choosing the 6 cards all in the same suitwhich is one way of getting a flush. There 6 ways of choosing 5 of theranks and 4 choices for the suit of these 5 ranks, and 3 choices for thesuit of the remaining card. This gives us choices of suits which produce a flush with 5 cards in the same suit.We remove these 76 choices which produce flushes giving us 4,020 choicesfor the 6 cards which do not produce a flush. Multiplying 4,020 by 1,645gives 6,612,900 high card hands.
If we sum the preceding numbers, we obtain 20,358,520 and we can be confidentthe numbers are correct.
Here is a table summarizing the number of 6-card poker hands. Theprobability is the probability of having the hand dealt to you whendealt 6 cards.
| hand | number | Probability |
| straight flush | 1,844 | .000091 |
| 4-of-a-kind | 14,664 | .00072 |
| full house | 165,984 | .00815 |
| flush | 205,792 | .0101 |
| straight | 361,620 | .0178 |
| 3-of-a-kind | 732,160 | .036 |
| two pairs | 2,532,816 | .1244 |
| pair | 9,730,740 | .478 |
| high card | 6,612,900 | .325 |
You will observe that you are less likely to be dealt a hand withno pair (or better) than to be dealt a hand with one pair. Thishas caused some people to query the ranking of these two hands.In fact, if you were ranking 6-card hands based on 6 cards, theorder of the last 2 would switch. However, you are basing the rankingon 5 cards so that if you were to rank a high card hand higher than a handwith a single pair, people would choose to ignore the pair in a6-card hand with a single pair and call it a high card hand. Thiswould have the effect of creating the following distortion. Thereare 16,343,640 6-card hands containing 5 cards which are high cardhands. Of these 16,343,640 hands, 9,730,740 also contain 5-cardhands which have a pair. Thus, the latter hands are more specialand should be ranked higher (as they indeed are) but would not beunder the scheme being discussed in this paragraph.
Poker Hand Probabilities Texas Hold Em
last updated 12 January 2000